

Below are the three Pythagorean identities in trigonometry. Pythagoras’s theorem states that in a right-angled triangle, the square of the hypotenuse equals the sum of the squares of the other two sides. It is easy to understand and prove the three Pythagorean identities of trigonometric ratios using the unit circle. \(\sin \theta = \frac\) Unit Circle Pythagorean Identities Applying this in trigonometry, we can find the values of the trigonometric ratio, as follows:
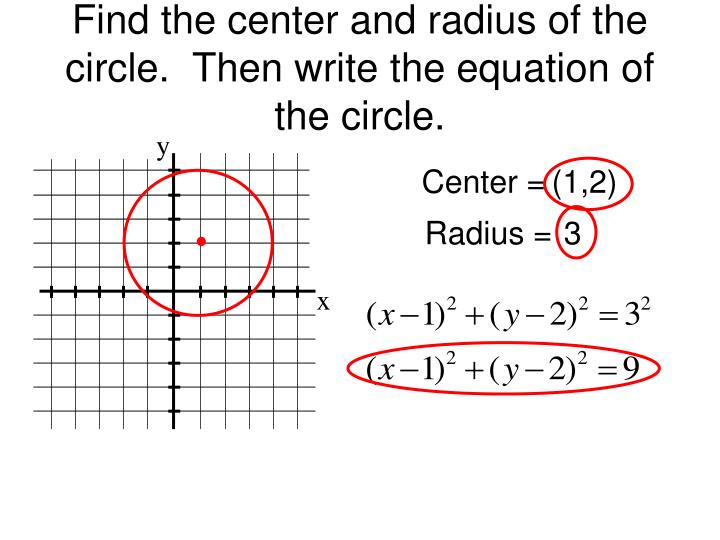
Now we have a right angle triangle with the sides \(1, x, y\). Here the values of \(x\) and \(y\) are the lengths of the base and the altitude of the right triangle. The radius vector makes an angle \(\theta\) with the positive x-axis and the coordinates of the endpoint of the radius vector are \((x, y)\). The radius of the circle represents the hypotenuse of the right triangle. Finding Trigonometric Functions Using a Unit Circle Imagine a right triangle placed in a unit circle in the cartesian coordinate system.
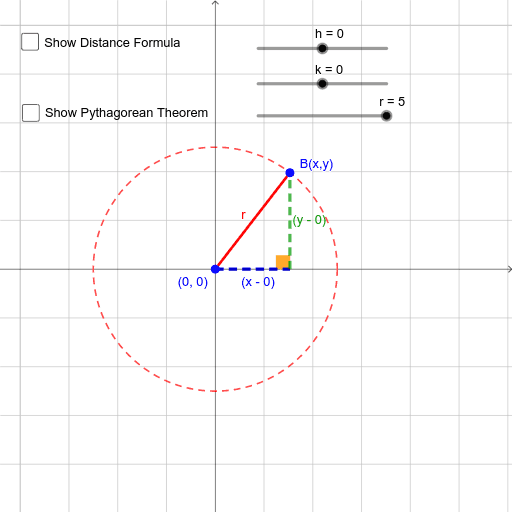
Applying Pythagoras’s theorem in a unit circle will help us understand trigonometric functions. Using a unit circle, we can calculate the trigonometric functions sine, cosine, and tangent. The above equation satisfies all the points lying on the circle across the four quadrants. Here for the unit circle, the center lies at \((0,0)\) and the radius is \(1\ unit\). Equation of a Unit CircleĮquation of a Unit Circle: \(x^2 + y^2 = 1\) This is simplified to obtain the equation of a unit circle. Hence the equation of the unit circle is \((x – 0)^2 + (y – 0)^2 = 1^2\). A unit circle is formed with its center at the point \((0, 0)\), which is the origin of the coordinate axes. This equation of a circle is simplified to represent the equation of a unit circle. The general equation of a circle is \((x – a)^2 + (y – b)^2 = r^2\), which represents a circle having the center \((a, b)\) and the radius \(r\). The locus of a point which is at a distance of one unit from a fixed point is called a unit circle. In trigonometry, the unit circle is useful for finding the trigonometric ratios sine, cosine, and tangent. The unit circle can be represented algebraically using the second-degree equation with two variables, x, and y. A unit circle is generally represented in cartesian coordinates. One unit circle is a circle with a radius of one unit.
#Circle equation calculator how to
Here we shall learn the equation of the unit circle, and understand how to represent each of the points on the circumference of the unit circle, with the help of trigonometric ratios of \(\cos \theta\) and \(\sin \theta\). In addition, a unit circle is useful for calculating the standard angles of all trigonometric ratios. In addition to having all the properties of a circle, the unit circle is also derived from the equation of a circle. A circle is a closed geometric figure that has no sides or angles. (x − 4.2408) 2 + (y − 2.4630) 2 = 4.3220 2.A unit circle is a circle with a unit radius from its name alone. The use of the matrix equation or the least squares circle calculator results in the following: Let's say we want to identify the equation of the circle that best fits the following four data points: (0, 1), (2, 5), (1, 6), and (7, 6). You can use the A, B, and C values to subsequently determine k, m, and r: In a situation in which the 3-by-3 matrix outlined on the left is invertible, the A, B, and C values are unique, and this determines the best fit circle. Where n is the number of data points (x i, y i). The circle regression model is supported by the following matrix equation: Once you have determined A, B, and C, it is possible to work backward to compute k, m, and r. As such, you can use the matrices to solve the least-squares problem. This results in a linear equation with the coefficients A, B, and C undetermined. The equation of the circle is linearized by the model ∂F/∂k = 0, ∂F/∂m = 0, and ∂F/∂r = 0. When you use the least-squares, you determine the "best fit" by minimizing the equation as follows:į(k, m, r) = ∑ 2 In a situation in which you have the data points x, y that are distributed in a ring-shape on an x-y plane, the least-squares regression can be used to determine the equation of a circle that will best fit with the available data points i.e., the following regression will help you to calculate the k, m, and r values of the curve:


 0 kommentar(er)
0 kommentar(er)
